Home /
Expert Answers /
Other Math /
c-distributive-equivalence-s-bvvd-avv-m-c-gt-d-d-conditional-equival-pa290
(Solved): c) Distributive Equivalence: (S^(^())(BvvD))/(Avv[M^(^())(C->D)]) d) Conditional Equival ...
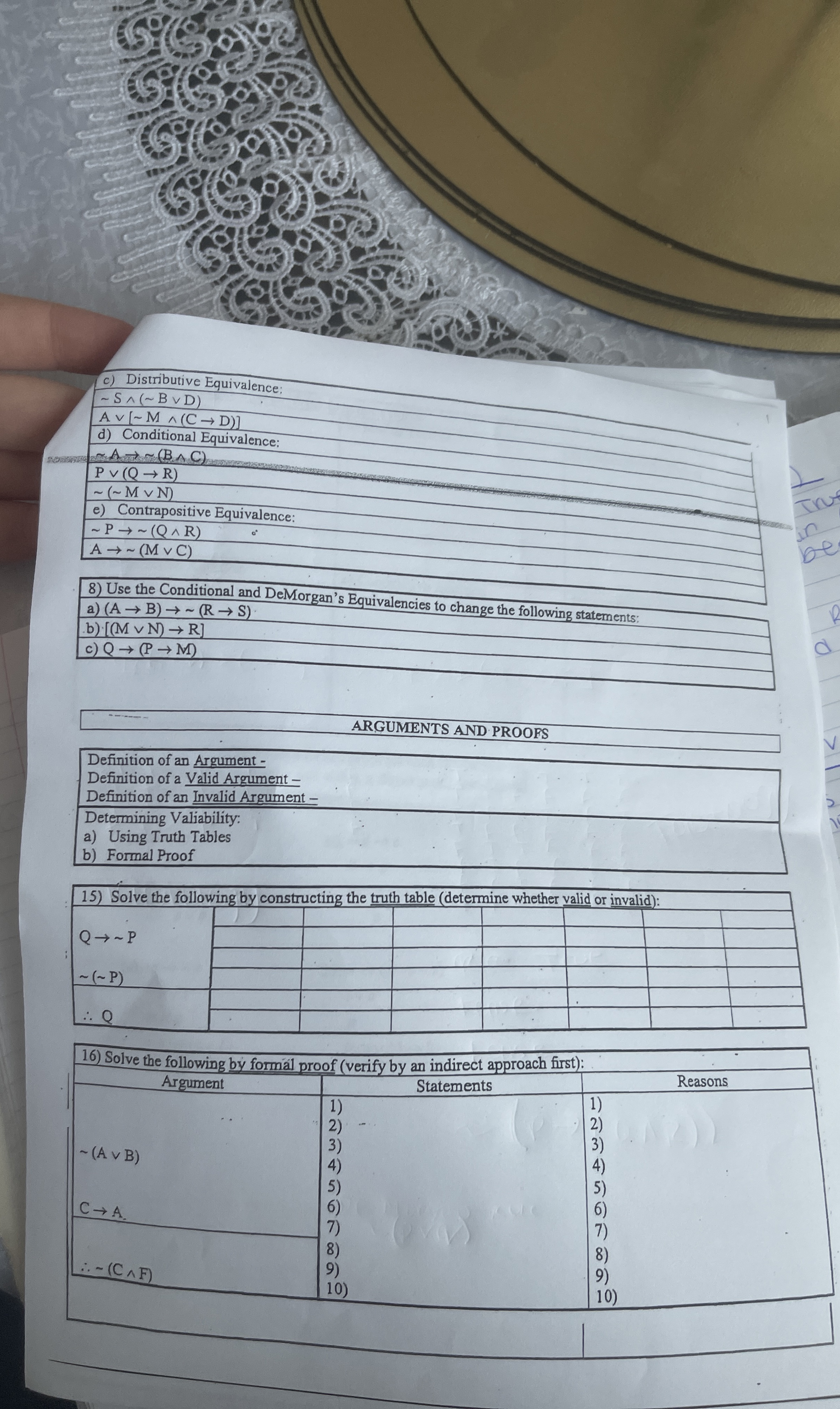
c) Distributive Equivalence:
(∼S^(^())(∼BvvD))/(Avv[∼M^(^())(C->D)])d) Conditional Equivalence:
∼A->∼(B^(^())C)
Pvv(Q->R)
∼(∼MvvN)e) Contrapositive Equivalence:
∼P->∼(Q^(^())R)
A->∼(MvvC)Use the Conditional and DeMorgan's Equivalencies to change the following statements: a)
(A->B)->∼(R->S)b)
(MvvN)->Rc)
Q->(P->M)ARGUMENTS AND PROOFS Definition of an Argument - Definition of a Valid Argument - Definition of an Invalid Argument - Determining Valiability: a) Using Truth Tables b) Formal Proof Solve the following by constructing the truth table (determine whether valid or invalid): Solve the following by formal proof (verify by an indirect approach first):